「統計的推測」とは? 支持率調査の理解から解説する
最終回となる今回は、これまで解説してきた知識を駆使しながら「統計的推測」を学ぶ。統計学を意思決定の際のコミュニケーションツールとして使いこなせるようになることが、エクゼクティブにとっての統計学の活用法だといえる。
信頼区間の便利な公式

倉田 博史
東京大学大学院総合文化研究科・教養学部 教授。
1996年一橋大学大学院経済学研究科理論経済学及び統計学専攻博士後期課程修了、博士(経済学)。山口大学経済学部助教授を経て現職。専門は統計学。著書に『Generalized Least Squares』(John Wiley and Sons)、「大学4年間の統計学を10時間でざっと学べる」(KADOKAWA)など。
全6回の連載も最終回となった。これまでの議論をごく簡単に振り返っておくと、第1回で統計学の根幹である「母集団と標本」の概念枠組みを紹介し、第2~4回の三回を使って、標本(つまりデータ)の情報の要約方法として平均・標準偏差、相関、回帰直線について学んだ。そして、第5回で母集団(つまり分析対象)の表現方法として確率分布を解説したという流れになる。つまり、これまで標本の情報のまとめ方と母集団の表し方について別個に議論してきたのである。最終回である今回は両者を結びつける作業、つまり標本の情報から母集団についての新たな知識を獲得する方法(これを統計的推測という)について解説し、議論の総仕上げとしたい。便利な公式を1つ紹介し、その仕組みを説明する。
例えば、A市の市長の支持率を調べるため、A市に住む有権者1000人を無作為に抽出し、市長を支持するか否かについて尋ねたところ、453人(=45.3%)が支持すると回答したとしよう。このとき、A市の有権者全体における支持率(これをpとおく)はおよそどれくらいか?
内閣支持率やテレビ番組の視聴率、生命保険の加入率など「~率」がデータ解析の対象となることは多い。これは「標本における比率」から「母集団における比率」を推測しようとする問題である。今の場合、有権者全体における支持率pがおよそ45.3%であることは明らかであろう。では、どれくらいの幅を見込めばよいか?答は
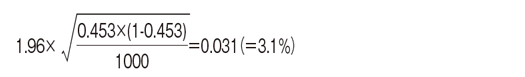
である。より正確に言えば、支持率pは確率95%で45.3±3.1(%)の範囲つまり「42.1(%)以上48.4(%)以下」の範囲に含まれる。このように、母集団における未知の量(今の場合は支持率p)を一定の確率(今の場合は95%)で含む範囲のことを信頼区間という。
公式の形で述べれば次の通りである。スマホの電卓でも計算できるので、会議中でも使える。ここで1.96は2で計算してもそれほど大きな違いではないので、面倒なときは2を使えばよい。

母平均と標本平均
上記の公式の仕組みも知っておこう。母集団と標本の枠組みで理解することが大切である。市長の支持率の例に戻って説明する。
各人の回答を、「支持する」を1、「支持しない」を0で表すと、0と1からなる1000個の数字の集まり(例えば、1,0,0,1,…,1,0というような)がデータとして得られる。この1000個の数字の集まりは母集団と標本のどちらになるであろうか。答は標本である。では、この標本を生み出した集団である母集団は何か。母集団は「その市に住む有権者の全体」である。
既に学んだ通り、母集団は確率分布で表現される。この母集団を表現する確率分布は前回学んだベルヌーイ分布である。

ここで、1(=支持)が出る確率pが有権者全体における市長の支持率である。このpは未知であるから、標本から推定する必要がある。どのようにすればよいだろうか。上の例では、1000人のうち453人(=45.3%)が支持すると回答したのでpを45.3%と推定した。
ここで、45.3%という推定値はデータの平均値に他ならない。何故なら、

となるからである。これは標本の平均値であるから、標本平均と呼ばれる。
他方、有権者全体における支持率pは母集団における平均値であり、母平均と呼ばれる。母平均とは確率分布の平均値(あるいは期待値)であって、次のように定義される:
母平均(期待値)=「取り得る値×確率」の総和
今の場合は次の通りである:
母平均=1×p+0×(1-p)=p
従って、我々が知りたいと考えている有権者全体における支持率は母集団の平均値つまり母平均であることが分かる。母平均は標本平均で推定できるのである。
コイン投げと2項分布
統計学では、「~率」のようなデータの分析をコイン投げに置き換えて扱う。例えば、市の有権者全体における支持率がpであるような市から1000人を選び、何人が市長を支持すると回答するかを数えることは、表が出る確率がpであるようなコインを1000回投げて何回表が出るかを観測することと同じと考えるのである。
このように考えれば、表の出る回数の確率分布も求められる。試しに、表が出る確率がp=0.5のコインを2回投げるときを考えてみよう。これは表と裏が同じ確率で出る歪みのないコインであるから一番考えやすい。表の出る回数は0,1,2の3通りがあり得て、それぞれの確率は次の表の通りとなる。

何故なら、起こり得る結果は、
(表,表), (表,裏), (裏,表), (裏,裏)
の4通りであり、それぞれの確率は1/4である。表が0回出る場合は(裏,裏)の1つだけだからその確率は1/4、表が1回出る場合は(表,裏), (裏,表)の2通りだから、その確率は2/4=1/2、表が2回出る場合は(表,表)の1つだけだからその確率は1/4である。
一般の場合はこれよりもかなり煩雑であるので、ここでは証明することはできないが、このような感じで求めればよいとだけ頭に入れておけばよい。「表が出る確率がpのコインをn回投げるときに表が出る回数」の確率分布を2項分布(binomial distribution)と言う。上の公式は2項分布の性質を使って導かれたものである。
エグゼクティブのための統計学
会議などの席上で、データ分析者の報告に対して何らかのコメントや判断をしなければならない立場にある方々にとって、よく分からないテクニカルな部分にどう対応すればよいのかというのは頭の痛い問題であると思う。分析結果を踏まえない、一般的なコメントを返すという対処の仕方もある。しかし、もしも管理職の方々が分析結果そのものを理解しようとする姿勢を示し、ストレートな質問やコメントをすれば、それがどんなに平易なものであれ分析者はそれを励みに思うだろう。会議の場も引き締まるはずである。エグゼクティブの方々にとって、統計学は数学でも情報技術でもなく、コミュニケーションツールである。是非、このツールを駆使して、意思決定の場を豊かなものにして頂きたいと思う。

